Consultorio de Matemáticas (Bonus: Química y Física)
Moderator: will-o-the-wisp
Re: Consultorio de Matemáticas (Bonus: Química y Física)
Yo creo que el problema es que Godah está generando las imágenes pero no está generando el link y está copiando directamente la imagen generada. Podría ser aixo?
悠久の風伝説
- Godah
- Cofre Sin Fondo

- Posts: 4431
- Joined: 14 Aug 2009, 10:09
- PSN ID: Queso_Godah
- Xbox Live ID: Godah
- Location: Pendulando entre Lleida y BCN
Re: Consultorio de Matemáticas (Bonus: Química y Física)
Efectivamente es lo que decía Viento. Muchas gracias por los avisos.  Ya está arreglado.
Ya está arreglado.
- Pappapishu
- Compañero de fatigas

- Posts: 11986
- Joined: 31 Jan 2010, 10:43
- PSN ID: Pappaìshu
- Twitter: @Pappapishu
- STEAM: pappapishu
- Location: Puerto Pollo, Isla Plunder
- Contact:
Re: Consultorio de Matemáticas (Bonus: Química y Física)
La tercera raiz no es dos elevado a tres (8), si no tres elevado a dos (9) ya que 7*8 = 56 y 7*9 = 63 entonces te quedaría, sin tener en cuenta las raíces:
1 - 2 + 3 = 2
1 - 2 + 3 = 2
Re: Consultorio de Matemáticas (Bonus: Química y Física)
Una duda gente, el dominio de definición de
Ln [x (cuadrado) - 1]
Es (1, + ¤¤), no?
Ln [x (cuadrado) - 1]
Es (1, + ¤¤), no?
- will-o-the-wisp
- Panacea Definitiva

- Posts: 2466
- Joined: 20 Dec 2009, 14:00
- PSN ID: oh_mike_dog
- Twitter: @oh_mike_god
- Location: Zaragoza
Re: Consultorio de Matemáticas (Bonus: Química y Física)
Para que el logaritmo tenga sentido, lo de dentro tiene que ser estrictamente positivo.
Por tanto,
[center]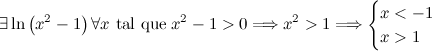 [/center]
[/center]
Entonces el dominio de definición es
[center]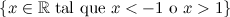 [/center]
[/center]
Que es lo mismo que poner
[center]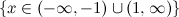 [/center]
[/center]
Es un error común pensar que la x tiene que ser siempre positiva dentro del logaritmo. Lo que tiene que ser positivo es lo de dentro (evidentemente si la función es log(x), x tiene que ser positiva).
Por tanto,
[center]
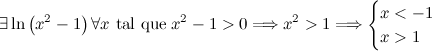 [/center]
[/center]Entonces el dominio de definición es
[center]
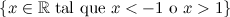 [/center]
[/center]Que es lo mismo que poner
[center]
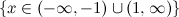 [/center]
[/center]Es un error común pensar que la x tiene que ser siempre positiva dentro del logaritmo. Lo que tiene que ser positivo es lo de dentro (evidentemente si la función es log(x), x tiene que ser positiva).
- will-o'-the-wisp

Re: Consultorio de Matemáticas (Bonus: Química y Física)
Oh, ya veo. Entonces, existe una asíntota vertical en el 0??
- will-o-the-wisp
- Panacea Definitiva

- Posts: 2466
- Joined: 20 Dec 2009, 14:00
- PSN ID: oh_mike_dog
- Twitter: @oh_mike_god
- Location: Zaragoza
Re: Consultorio de Matemáticas (Bonus: Química y Física)
Existen dos asíntotas verticales (en -1 y 1). Baja de forma logarítmica desde el infinito hasta menos infinito al llegar a x=-1. Luego no hay nada hasta que sube desde menos infinito en x=1 al infinito de forma logarítmica.
- will-o'-the-wisp

Re: Consultorio de Matemáticas (Bonus: Química y Física)
Ahora en el mismo ejercicio me he quedado atascado encontrando las asintotas oblicuas.
Se supone que :
Y= mx + n
Para averiguar m:
Lim cuando X - > ¤¤
De f(x) /x
Donde f(x), es Ln(x2 - 1). El 2 es un cuadrado.
Lim x - > ¤¤ de Ln ¤¤/ ¤¤
Igual a 1. Ln ¤¤ = ¤¤
¤¤/¤¤ = 1
Para averiguar n
Lim x -> ¤¤ de f(x) - mx
Donde m=1
Me queda ¤¤ - ¤¤
(ln ¤¤ = ¤¤) - (1 por X = X) dónde X = ¤¤
Y ahí me he quedado.
Se supone que :
Y= mx + n
Para averiguar m:
Lim cuando X - > ¤¤
De f(x) /x
Donde f(x), es Ln(x2 - 1). El 2 es un cuadrado.
Lim x - > ¤¤ de Ln ¤¤/ ¤¤
Igual a 1. Ln ¤¤ = ¤¤
¤¤/¤¤ = 1
Para averiguar n
Lim x -> ¤¤ de f(x) - mx
Donde m=1
Me queda ¤¤ - ¤¤
(ln ¤¤ = ¤¤) - (1 por X = X) dónde X = ¤¤
Y ahí me he quedado.
- will-o-the-wisp
- Panacea Definitiva

- Posts: 2466
- Joined: 20 Dec 2009, 14:00
- PSN ID: oh_mike_dog
- Twitter: @oh_mike_god
- Location: Zaragoza
Re: Consultorio de Matemáticas (Bonus: Química y Física)
No es cierto que infinito entre infinito sea 1. La comparación de infinitos se realiza antes de hacer el límite. Voy a simplificarlo con unas reglas de comparación de infinitos:
[spoiler]· Exponencial (a^x, a>1) > Potencial (x^m) > Logarítmica (log(x))
· El orden de una exponencial es mayor que el de otra exponencial si su base es mayor. Dos exponenciales con la misma base son del mismo orden.
· El orden de una potencial es mayor que el de otra potencial si su exponente es mayor. Dos polinomios son del mismo orden si el grado de su término mayor es el mismo.
· Al solucionar infinito/infinito, puede ocurrir que el resultado sea infinito (si el numerador es de orden mayor), cero (si el denominador es de orden mayor) o un número finito (si ambos son del mismo orden).[/spoiler]
En este caso tenemos
[center]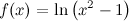 [/center]
[/center]
La asíntota oblícua será una recta con ecuación
[center]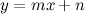 [/center]
[/center]
Averigüemos m:
[center]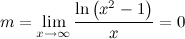 [/center]
[/center]
Esto es porque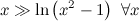 (el denominador es de orden mayor).
(el denominador es de orden mayor).
Que una recta tenga pendiente 0 implica que es horizontal.
Vamos con n:
[center]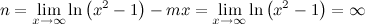 [/center]
[/center]
Que una función tenga ordenada en el origen en el infinito indica, explicado de forma un poco brusca, que está tan arriba que no existe.
Por tanto, no hay ni asíntota oblícua ni horizontal. De hecho, la función tiene más o menos esta gráfica:
[center] [/center]
[/center]
[spoiler]· Exponencial (a^x, a>1) > Potencial (x^m) > Logarítmica (log(x))
· El orden de una exponencial es mayor que el de otra exponencial si su base es mayor. Dos exponenciales con la misma base son del mismo orden.
· El orden de una potencial es mayor que el de otra potencial si su exponente es mayor. Dos polinomios son del mismo orden si el grado de su término mayor es el mismo.
· Al solucionar infinito/infinito, puede ocurrir que el resultado sea infinito (si el numerador es de orden mayor), cero (si el denominador es de orden mayor) o un número finito (si ambos son del mismo orden).[/spoiler]
En este caso tenemos
[center]
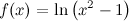 [/center]
[/center]La asíntota oblícua será una recta con ecuación
[center]
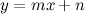 [/center]
[/center]Averigüemos m:
[center]
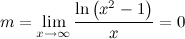 [/center]
[/center]Esto es porque
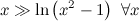 (el denominador es de orden mayor).
(el denominador es de orden mayor).Que una recta tenga pendiente 0 implica que es horizontal.
Vamos con n:
[center]
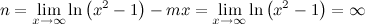 [/center]
[/center]Que una función tenga ordenada en el origen en el infinito indica, explicado de forma un poco brusca, que está tan arriba que no existe.
Por tanto, no hay ni asíntota oblícua ni horizontal. De hecho, la función tiene más o menos esta gráfica:
[center]
 [/center]
[/center]- will-o'-the-wisp

Re: Consultorio de Matemáticas (Bonus: Química y Física)
Muchas gracias Will. Gracias a tu ayuda lo resolví.








