Dividiendo tal cual como dices te va a dar:
[center]
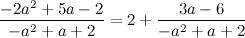
[/center]
Y no se puede seguir a menos que factoricemos. Por tanto, voy a explicar la factorización desde el principio y luego lo vamos a aplicar aquí.
Sea
p(
z) un polinomio de grado
n (
n>0):
[center]
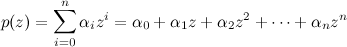
[/center]
Donde los
α_i son los coeficientes que acompañan a las
z (pueden ser cero todos, excepto
α_n, que es requisito que no sea nulo para que en el polinomio aparezca
z^
n y sea de grado
n).
El
teorema fundamental del álgebra dice esencialmente:
Todo polinomio de grado n tiene exactamente n raíces complejas.
Dicho de otro modo, si p(z) es un polinomio de grado n, entonces la ecuación p(z)=0 tiene exactamente n soluciones complejas.
Dos cosas:
- Estas raíces pueden no ser únicas. Por ejemplo, el polinomio
x^2-4
x+4 tiene como raíz doble
x=2.
- No te asuste que diga que las raíces son complejas en vez de reales. Para lo que vamos a ver a partir de aquí, los dos conjuntos se usan de la misma forma. A partir de ahora utilizaré solamente polinomios reales, pero todo lo que voy a decir es aplicable también a polinomios con variable compleja.
Sigamos. Sea el polinomio real
p(
x) de grado
n y sean
x_1,
x_2...,
x_n sus raíces (es decir, las soluciones de
p(
x)=0), entonces
p(
x) se puede expresar como:
[center]
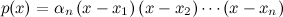
[/center]
Si te fijas, aparece suelto el coeficiente del término que marca el grado del polinomio. Cada factor que contiene
x se denomina
polinomio irreductible y son de grado uno. Vamos a hacer un ejemplo de segundo y otro de tercer grado:
Ejemplo 1.
[center]
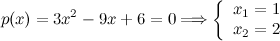
[/center]
Por tanto,
[center]
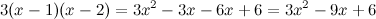
[/center]
Ejemplo 2.
[center]
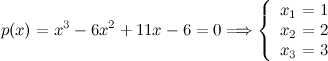
[/center]
Por tanto,
[center]
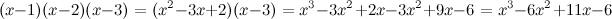
[/center]
Cuando dividimos números muy largos, es aconsejable ver si contienen factores comunes antes de realizar la división. Por ejemplo, si tuviéramos que dividir 8768782 entre 648764, comprobaríamos que ambos contienen el factor 2 y nuestra división sería entre números más pequeños (si no quisiéramos el resultado exacto, sino la fracción más simple, entonces habría que repetir esto hasta que no hubiera factores comunes).
A la hora de dividir polinomios ocurre lo mismo. Supongamos dos polinomios
p(
x) (de grado
n) y
q(
x) (de grado
m).
p(
x) tiene raíces
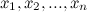
y
q(
x) tiene raíces
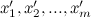
[center]
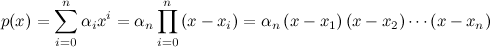
[/center]
[center]
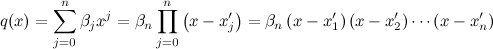
[/center]
Para que los polinomios sean divisibles, al menos uno de estos factores tiene que ser común. Supongamos que comparten una raíz
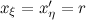
[center]
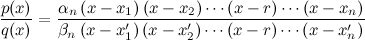
[/center]
En este caso, simplificaríamos los (
x-
r). Si ambos polinomios compartieran más raíces, esto se repetiría hasta que ya no se pudiera simplificar más.
Esta es la teoría que voy a aplicar en el ejercicio, que voy a poner en otro post para que esté más organizado.
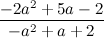
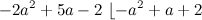







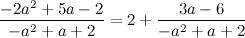 [/center]
[/center]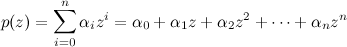 [/center]
[/center]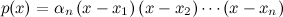 [/center]
[/center]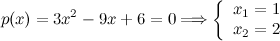 [/center]
[/center]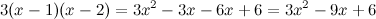 [/center]
[/center]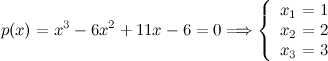 [/center]
[/center]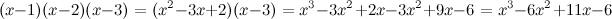 [/center]
[/center]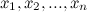 y q(x) tiene raíces
y q(x) tiene raíces 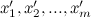
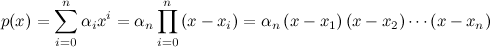 [/center]
[/center]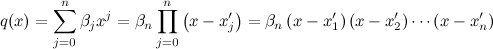 [/center]
[/center]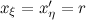
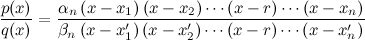 [/center]
[/center]
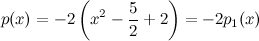 [/center]
[/center]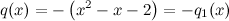 [/center]
[/center]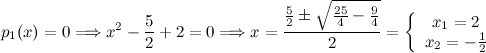 [/center]
[/center]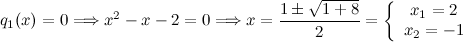 [/center]
[/center]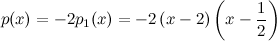 [/center]
[/center]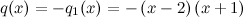 [/center]
[/center]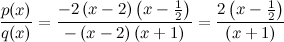 [/center]
[/center]

 A mí me asalta una duda ahora mismo: cuando se necesita factorizar un polinomio con un número entero muy elevado (me refiero al número sin X, vaya) como 30, hay muchos divisores que emplear para la regla de Ruffini. ¿Hay algún método para acortar este paso y saber qué divisores nos pueden servir? Es que si no hay que empezar por 1, -1, 2, -2 y se hace largo...
A mí me asalta una duda ahora mismo: cuando se necesita factorizar un polinomio con un número entero muy elevado (me refiero al número sin X, vaya) como 30, hay muchos divisores que emplear para la regla de Ruffini. ¿Hay algún método para acortar este paso y saber qué divisores nos pueden servir? Es que si no hay que empezar por 1, -1, 2, -2 y se hace largo...
 [/center]
[/center] [/center]
[/center] [/center]
[/center] [/center]
[/center] [/center]
[/center] [/center]
[/center] [/center]
[/center]


 [/center]
[/center] [/center]
[/center]